Diffie-Hellman Algorithm

[ˈdɪfɪ ˈhelmən]
алгоритм Диффи-Хеллмана
 Алгоритм (Algorithm) открытого распределения ключей (Key Distribution), также называемый экспоненциальным распределением ключей (Exponential Key Agreement). Первый известный алгоритм с применением открытого ключа (Public Key). Использует дискретные логарифмы в конечных полях. Основан на использовании односторонней показательной функции f (x) = a^x mod n. Опубликован в 1976 г. в статье «Новые направления в криптографии». Применяется для распределения криптографических ключей по незащищённым каналам связи. Для выработки ключа, используемого для шифрования информации пользователи (например, A и B) должны сделать следующее:
 1. Пользователи A и B независимо выбирают случайные числа KA и KB из интервала от 1 до p–1, причём p — простое число. Числа KA и KB называются секретными ключами (Private Key).
 2. Пользователи A и B вычисляют:
Y_A = g^KA mod p
 и

Y_B = g^KB mod p,
причём значения g и p являются известными всем абонентам системы обмена сообщениями и 1 < g < p. Числа YA и YB называются открытыми ключами. Число g называется генератором.
 3. Пользователи A и B обмениваются открытыми ключами по незащищённому каналу связи.
 4. По полученным открытым ключам, каждый из пользователь независимо вычисляет секретный параметр K, который и является общим сеансовым секретным ключом, который может использоваться для шифрования.
 Для пользователя A:
 

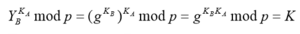
 Для пользователя B:
 

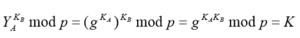
 Недостаток схемы Диффи-Хеллмана — необходимость аутентификации (Authentication) открытых ключей пользователей в п. 3, то есть подтверждения того, что ключи YA и YB действительно выработаны пользователями A и B.

— Игорь Мостицкий (обсуждение) 13:39, 9 января 2026 (MSK)